滑輪

                                            資料來源：教育部學加油站、維基百科

滑輪

約從西元前五世紀起，希臘人使用滑輪在船上或戲院中工作，幫助人類節省體力的消耗。滑輪通常是一個具有溝槽邊緣的心輪，溝槽上有繩子通過以利於人工操作。常用於省力的舉起重物，或為了方便而改變施力點和方向。

定滑輪和動滑輪可用許多不同組合方式得到滑輪組，不同的滑輪組有不同的機械利益比。換個說法，滑輪系統中機械利益比是由滑輪的數目與組成位置而決定。

*************************************************************************

用於小型船舶貨物裝卸的滑車裝置，滑輪是其重要組件。

        在力學裏，典型的滑輪（pulley）是可以繞著中心軸旋轉的圓輪。在圓輪的圓周面具有凹槽，將繩索纏繞於凹槽，用力牽拉繩索兩端的任一端，則繩索與圓輪之間的摩擦力會促使圓輪繞著中心軸旋轉。[1]按滑輪中心軸的位置是否移動，可將滑輪分為「定滑輪」、「動滑輪」；定滑輪的中心軸固定不動，動滑輪的中心軸可以移動。滑輪主要的功能是牽拉負載、改變施力方向、傳輸功率等等。多個滑輪共同組成的機械稱為「滑輪組」，或「複式滑輪」。滑輪組的機械利益較大，可以牽拉較重的負載。滑輪也可以成為鏈傳動或帶傳動的組件，將功率從一個旋轉軸傳輸到另一個旋轉軸。

歷史

關於滑輪的繪品最早出現於一幅西元前八世紀的亞述浮雕。這浮雕展示的是一種非常簡單的滑輪，只能改變施力方向，主要目的是為了方便施力，並不會給出任何機械利益。在中國，滑輪裝置的繪製最早出現於漢代的畫像磚、陶井模。^[2][3][4]在《墨經》裏也有記載關於滑輪的論述。^{[註 1][5]}
  古希臘人將滑輪歸類為簡單機械。^[6]早在西元前400年，古希臘人就已經知道如何使用複式滑輪了。大約在西元前330年，亞里斯托德在著作《機械問題》（《Mechanical Problems》）裏的第十八個問題，專門研討「複式滑輪」系統。阿基米德貢獻出很多關於簡單機械的知識，詳細地解釋滑輪的運動學理論。^[7]據說阿基米德曾經獨自使用複式滑輪拉動一艘裝滿了貨物與乘客的大海船。^[8]西元一世紀，亞歷山卓的希羅分析並且寫出關於複式滑輪的理論，證明了負載與施力的比例等於承擔負載的繩索段的數目，即「滑輪原理」。
1608年，在著作《數學紀要》（《Mathematical Collection》）裏，荷蘭物理學者西蒙·斯特芬表明，滑輪系統的施力與負載之間移動路徑的長度比率，等於施力與負載之間的反比率。這是雛型的虛功原理。
1788年，法國物理學者約瑟夫·拉格朗日在鉅著《分析力學》（《Mécanique analytique》）裏，使用滑輪原理推導出虛功原理，從而揭起了拉格朗日力學的序幕。^[9]

操作理論

為了簡易分析起見，假設滑輪和繩索的重量為零，不會因摩擦而損失任何能量，繩索也不會被延伸拉長。

定滑輪

定滑輪系統。

定滑輪的中心軸固定不動。定滑輪的功能是改變力的方向。當牽拉重物時，可使用定滑輪將施力方向轉變為容易出力的方向。使用定滑輪時，施力牽拉的距離等於物體上升的距離，不能省力也不費力。繩索兩端的拉力相等，所以，輸出力等與輸入力，定滑輪的機械利益等於1。

動滑輪

動滑輪系統。	受力簡圖。

動滑輪的中心軸可以移動。動滑輪不能改變施力方向。在靜力平衡時，作用於滑輪的淨力必需等於零。另外，繩索兩端的拉力相等。所以，在繩索每一端的拉力等於負載的一半。假設，將繩索的一端繫綁於一固定點，則用拉力 於繩索的另一端，就可以提升負載 。若要把負載提升高度 ，則必須在繩子的自由端往上方拉動 的距離。

課外補充

滑車組

由定滑車與動滑車以繩索纏繞牽引組成的各種各樣的滑車組。^[10]

定義「滑車」為一組中心軸同軸的滑輪。按照滑輪數目不同，滑車可以分為單門滑車、雙門滑車和多門滑車。按滑車中心軸的位置是否移動，可將滑車分為「定滑車」、「動滑車」：定滑車的中心軸固定不動，動滑車的中心軸可以移動。如右圖所示，滑車組是由定滑車與動滑車以繩索穿繞組成，^[11][12]定滑車懸掛於上方的固定點，動滑輪吊掛著下方的負載。繩索穿繞的方法有幾種。繩索被繫縛的一端稱為「終結端」，可以繫縛於定滑車或動滑車；另一端稱為「自由端」，是施力處。
滑車組的機械利益等於承擔動滑輪與其負載的繩子數目。在右圖中的各種各樣滑車組的機械利益分別為^[10]

• 1－1滑車組（單門動滑車，單門定滑車，定端頭固定於定滑車）：2
• 1－2滑車組（單門動滑車，雙門定滑車，定端頭固定於動滑車）：3
• 2－2滑車組（雙門動滑車，雙門定滑車，定端頭固定於定滑車）：4
• 2－3滑車組（雙門動滑車，三門定滑車，定端頭固定於動滑車）：5
• 3－3滑車組（三門動滑車，三門定滑車，定端頭固定於定滑車）：6

滑車組的特性是使用單獨一條繩索來傳輸張力，通過一個或多個滑輪，達成提升或移動負載的目的。假設繩索的質量為零，則繩索的任意位置所感受到的張力都一樣。假設滑車組系統不耗散或儲存能量，則其機械利益等於作用於負載的拉力的數目。計算這數目很簡單。首先，滑車組的每一個滑輪只能有一條繩索纏繞於其凹槽，這可以當作從滑輪引出兩條繩索段。另外，終結端被繫縛的滑車，可當作從滑車引出一條繩索段。由於每一條繩索段都是同樣繩索的一部分，承擔負載的每一條繩索段都會施加同樣的拉力於負載，所以，機械利益等於從負載引出的繩索段的數目。
假設一個滑車所吊掛的負載為 ，從這滑車引出的繩索段數目為 ，則在靜力平衡下，每一條繩索段的拉力為 ，這意味著輸入力為 。因此，這滑車組能夠減少輸入力的因子為 ，機械利益為 。

1－1滑車組

如左圖所示，左邊是1－1滑車組繪圖，右邊是將滑車組的滑輪分離後的受力簡圖。對於1－1滑車組，下方動滑車吊掛的負載為 ，從這動滑車引出的繩索段數目為 ，所以輸入力為 ，機械利益為 。
注意到左邊1－1滑車組繪圖並不很正確，從終結端到動滑輪的繩索段不呈垂直方向，因此其牽拉動滑輪的拉力具有水平分量，由於沒有其它作用力能夠抵消這水平拉力，所以這滑車組不處於靜力平衡，動滑輪會往旁邊移動，使得水平拉力能被抵消。這瑕疵所造成的誤差不大，可以被忽略，前面所做數值分析大約正確。

2－2滑車組

如左圖所示，左邊是2－2滑車組繪圖，右邊是將滑車組的滑輪分離後的受力簡圖。對於2－2滑車組，下方動滑車吊掛的負載為 ，從這動滑車引出的繩索段數目為 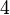，所以輸入力為 ，機械利益為 。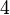
注意到左邊2－2滑車組繪圖並不很正確，詳盡細節請參閱先前1－1滑車組段落。